Complex Systems Thinking: Learning and Logic Amid Chaos and Uncertainty
- Eunomia Journal

- Apr 23, 2020
- 6 min read
By
John J. McKeown
Introduction
A great deal of scholarship has developed in the course of understanding and framing complicated events for analysis. Examples of subjects include armed conflict, migration, and international trade. If we consider these phenomena as a system where many individual parts interact to cause some greater, observable, state we can apply a certain type of thinking to help us visualize and understand them. These situations may consist of competing goals or interests, incomplete information about the system, or unknown influences – all within a web of relationships that continuously interact and appear random or even chaotic. These are referred to generally as complex systems.
Definition
A complex system can be defined as a collection of inter-related (causal) items, internal feedback mechanisms, non-linearities, delays, and uncertainties (Spector, Christensen, Sioutine, & McCormack, 2001). Further, Eseryel, Ifenthaler & Ge (2013), provide six features of complex systems: 1. Complexity due to a large number of variables, 2. Connectivity of variables, 3. Intransparency of variables, 4. Time-delayed effects, 5. Dynamic developments, 6. Multiple goals. Thus, the system issue or problem is ill-defined and lacks a discrete right or wrong answer or conclusion. Think of an economic system, political system, or natural phenomenon and relate its components to this definition.
Knowledge Construction
Let’s quickly examine how we develop knowledge and understanding. Our brains are exceptionally efficient at processing and recalling things we have learned. Knowledge organization is referred to as schemas which help achieve efficiency in working (short term) memory processing of new information by allowing new elements to be processed simply. Schemas held in long term memory are crucial for solving complex problems. In an environment where there is a great deal of interactivity among the information elements the channels of working memory can become overloaded, impairing the learning process. This interactivity is driven by the requirement that one understand all elements involved simultaneously in order for any one element to have meaning. Alternatively, information elements with low interactivity can be processed simply. So, as the demands on working memory increase with high element interactivity subjects like complex systems, the mind employs already developed schemas to allow for these elements to be processed as a single element. Logical reasoning structures and comparative structures may be more apt to be applied in other domains. This transference allows for growth of subsequent knowledge structures outside of the original context.
Logic
Domain experts and novices will tend to apply different methods for constructing models for understanding of complex systems (Shin, 2016). For example, novices may tend to use fewer concepts (or irrelevant ones) in building mental models (Spector et al., 2001). As well, different methods of reasoning may be more natural for experts and novices. Sweller, Jeroen, van Merrienboer &. Paas (1998) suggest that experts are more apt to employ inductive reasoning while novices seem more comfortable with deductive approaches. In an environment that is characterized by ill-structured problems and continuous interactions (rather than discrete events), abductive reasoning can be used to identify the most likely relationships between multiple causes and effects.
Abductive reasoning considers general observations and yields the most likely hypothesis for cause but not necessarily the “truth” since we are talking about many factors and unstable relationships. Also, effective systems thinking diverges from what many consider a conditioned (by the education system) predisposition for reductionist thinking. This is the tendency to try to break down large problems into smaller, understandable components (Marciano et al., 2014). Linear absolutes that contemplate only discrete events miss the essence of a system characterized as a continuous interaction of elements that result in “emergent behaviors” (Marciano et al., 2014, p.23). These are collective effects resulting from the relationships between multiple system components (i.e., a flock of birds flying precise movements in formation with split-second timing). It is the observation about that behavior that is the reason for our interest in the system the first place.
Mapping for Understanding
As noted, the system is dynamic and uncertain. Mental models that represent them are referred to as the “problem space” (Eseryel, et al., 2013, p.445).A method for visually representing the causal directionality and magnitude of the relationships between elements in the system is known as causal mapping. Jonassen (2011) states that the cognitive processes used to help learners solve problems are constructing mental models, analogical reasoning, and argumentation. Learners construct models and apply them to problems rather than applying logical rules (Jeong & Lee, 2011). Causal maps identify the perceptions of cause (Nadkarni & Shenoy, 2004). A simple example can show the magnitude of causal relationships between elements with bold lines and represent a relative magnitude visually of the scope and prominence of individual elements (see figure 1).

In this example, we evaluate the effects of various phenomena associated with conflict. Each has a relationship to the other with different and variable causal directions and magnitude. Here, warfare sometimes causes migration while famine usually causes migration and famine and warfare can cause one another. One can also represent the change in the nature of events or elements in the system over time. For example, one can capture when an element ceases to be a unique component and simply becomes an aspect of another as that element becomes more prominent (see figure 2).
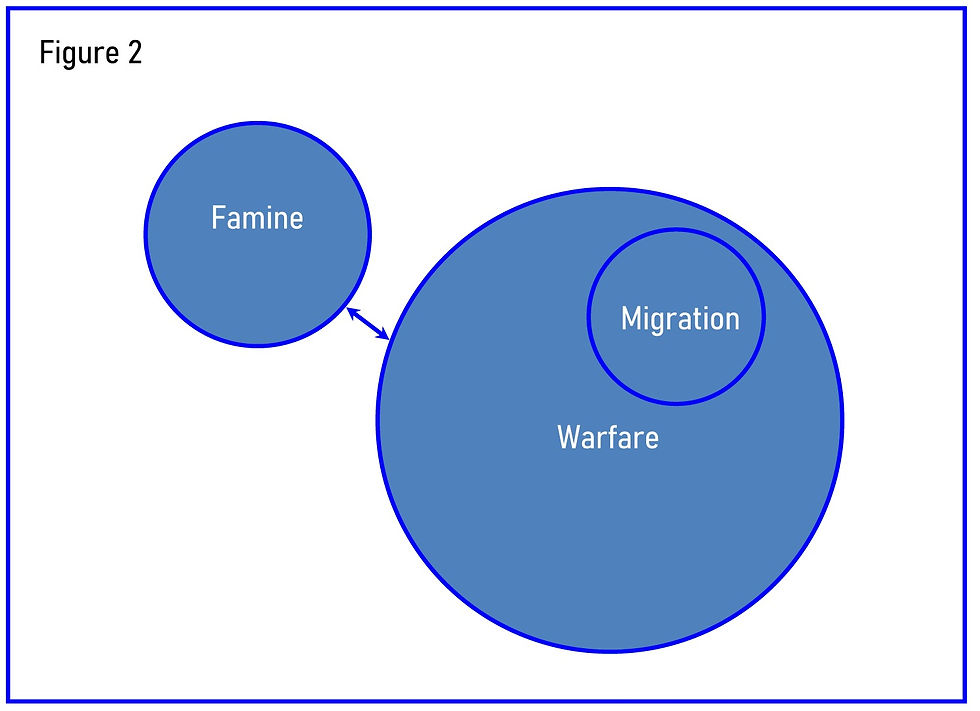
Map construction as an exercise requires reflective thinking and a tolerance for alternative truths and contradictions (Merriam et al., 2012). By referring to a “problem space”, we may suggest or expect a solution. In fact, problem finding, exploring, and critical examination to illicit deep understanding of the complex system is itself the objective. An exercise like mapping can help develop durable knowledge structures. Its construction facilitates autonomous and generative learning which establishes these structures. Map construction is more impactful on learning than being given an expert constructed map (Shin, 2016). In fact, these maps were more effective as a learning instrument for low prior knowledge learners that those with high levels of prior knowledge. One reason may be that with high levels of prior knowledge there are already mental models in place that might inhibit the process of integrating new information (O’Donnell, Dansereau, & Hall, 2002).
Assessment
There is a tendency to try to measure and quantify how well causal maps capture a complex system or the underlying domain knowledge. Historically, domain knowledge tests have been used to measure systems thinking (Eseryel et al., 2013). There is a notion of correctness to the measure. Our purpose is to understand the system and since we are examining a web of events and relationships, another school of thought is to use narratives. We learn from “storying” our experiences (Merriam et al., 2012, p.188). Annetta (2011) suggests that evaluating complex, conditionally causal relationships cannot be accomplished with a linear or binary method. There is a place for abstract observation to determine the quality of structural knowledge and causal reasoning (Eseryel et al., 2013). So, one should consider a map’s utility from the standpoint of reason and then discuss, engage, and critique through interactions with others. This will help facilitate deep learning and greater insight into the seemingly chaotic and unstable environment of complex systems.
About the Author
John McKeown is prior service civil affairs with many years of experience in education administration and public finance. John has earned a B.S., M.S., C.A S. and completed PhD work in the Learning Sciences. He is also currently an adjunct professor of finance at the University of Maryland Global Campus.
References
Spector, J. M., Christensen, D. L., Sioutine, A. V., & McCormack, D. (2001). Models and simulations for learning in complex domains: Using causal loop diagrams for assessment and evaluation. Computers in Human Behavior,17(5), 517-545.
Eseryel, D., Ifenthaler, D., & Ge, X. (2013). Validation study of a method for assessing complex ill-structured problem solving by using causal representations. Educational Technology Research and Development, 61(3), 443-463. doi:10.1007/s11423-013-9297-2
Shin, H. S. (2016). Examining the relationship between prior knowledge, causal maps, and causal mapping processes (Order No. 10240424). Available from ProQuest Dissertations & Theses Global. (1873488256). Retrieved from https://search-proquest-com.gate.lib.buffalo.edu/docview/1873488256?accountid=14169
John Sweller, Jeroen J. G. van Merrienboer and Fred G. W. C. Paas. Cognitive Architecture and Instructional Design. Educational Psychology Review, Vol. 10, No. 3 (September 1998), pp. 251-296
Marciano, J. N., Leonardo Cunha de Miranda, & Erica Esteves Cunha de Miranda. (2014). Evaluating multiple aspects of educational computer games: Literature review and case study. International Journal of Computer Games Technology, 2014, 1-12. doi:10.1155/2014/139205
Jeong, A., & Lee, W. J. (2012). Developing causal understanding with causal maps: The impact of total links, temporal flow, and lateral position of outcome nodes. Educational Technology Research and Development, 60(2), 325-340. doi:10.1007/s11423-011-9227-0
Nadkarni, S., & Shenoy, P. P. (2004). A causal mapping approach to constructing bayesian networks. Decision Support Systems, 38(2), 259-281. doi:10.1016/S0167-9236(03)00095-2
Merriam, S. B., Caffarella, R. S., & Baumgartner, L. M. (2012). Learning in adulthood: A comprehensive guide. John Wiley & Sons.
O'Donnell, A. M., Dansereau, D. F., & Hall, R. H. (2002). Knowledge maps as scaffolds for cognitive processing. Educational Psychology Review, 14(1), 71-86. doi:10.1023/A:1013132527007
Annetta, L. B. S. (2011). Serious Educational Game Assessment: Practical Methods and Models for Educational Games, Simulations and Virtual Worlds. Rotterdam: SensePublishers. Retrieved from http://ebookcentral.proquest.com/lib/buffalo/detail.action?docID=974162
Cite this Article
Note:
John McKeown, "Complex Systems Thinking: Learning and Logic Amid Chaos and Uncertainty," Eunomia Journal (April 2020): https://www.civilaffairsassoc.org/post/complex-systems-thinking-learning-and-logic-amid-chaos-and-uncertainty
Bibliography:
McKeown, John. "Complex Systems Thinking: Learning and Logic Amid Chaos and Uncertainty." Eunomia Journal, (April 2020): https://www.civilaffairsassoc.org/post/complex-systems-thinking-learning-and-logic-amid-chaos-and-uncertainty






